Lecture 3: Piping & Grouped Comparisons
Introduction
Consider the following graph, which plots each pitcher’s Earned Run Average (ERA) by year, along with a line showing the average ERA for each year.
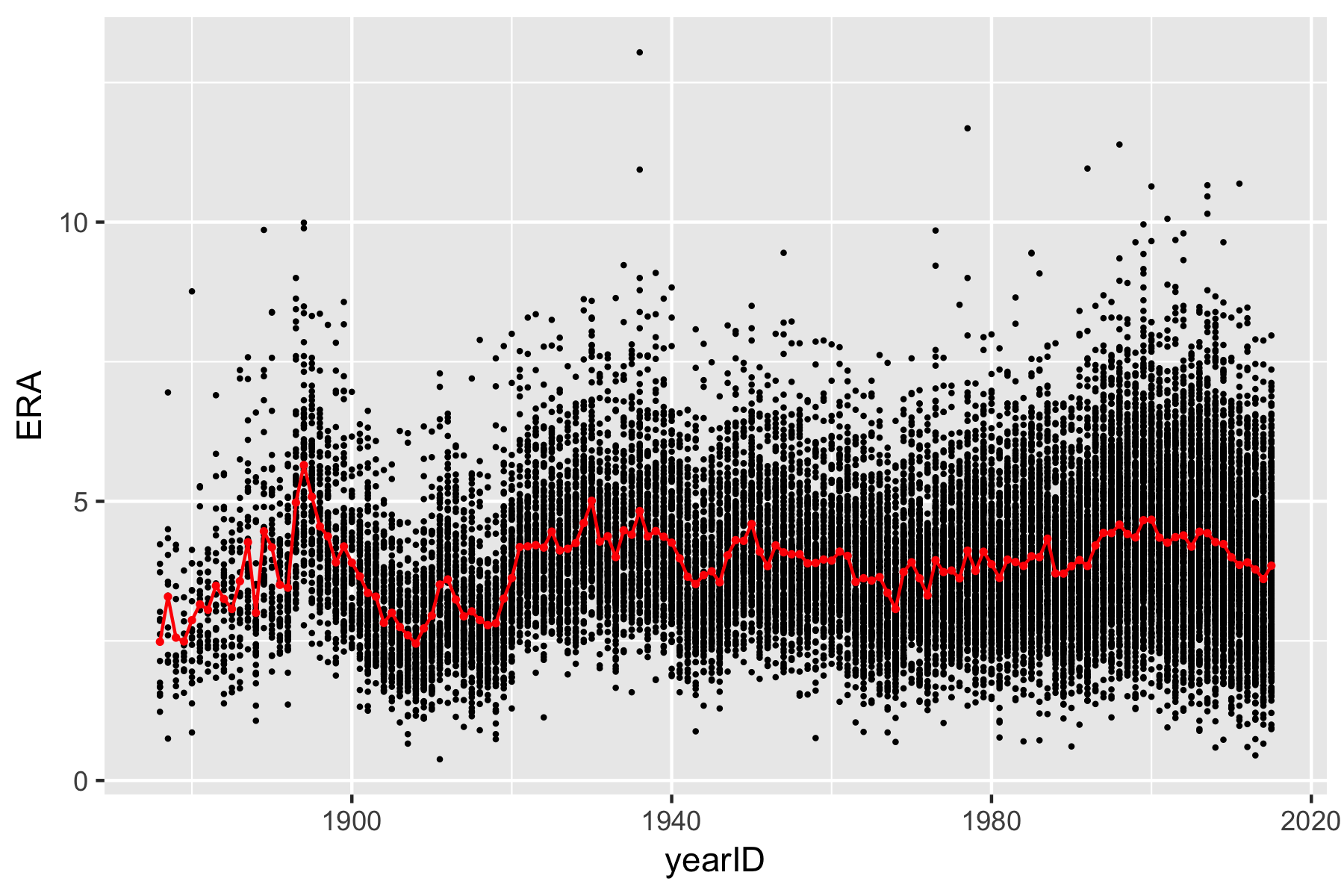
In order to create this figure we need to be able to compute the mean
ERA in each year. In Lecture 2, we computed
average statistics for a single NBA season in two steps. First, we used
filter() to create a new tbl containing only the data from
that particular season. Then we used reframe() to compute
the desired averages. To compute the mean ERA in each season, we
certainly could proceed in a similar way. But this would be incredibly
tedious. Luckily there is an easier way in dplyr.
In order to reproduce this image, we will work with the Lahman Baseball Database. As it turns out, there is an R package that includes the entire database (up until the 2016 season). We will load that into R along with the tidyverse packages when we begin our analysis.
Piping
Data analysis can usually be described as set of functions or
operations being applied to a dataset in sequence. In Problem Set 2, filter() and
select() were applied in sequence to the tbl
hitting_qualified. Each of these functions takes a tbl as
an input and returns a different tbl as an output. More complex data
analysis tasks often require sequences of several operations on the
dataset. Given what we have learned so far, it would appear that the
analyst has two options: (1) save a temporary tbl after each function
application and apply the next function to the temporary tbl or (2)
“nest” all of the functions together. Below is an example of what these
two strategies look like:
# An Example: Applying func_1(), func_2(), and func_3() sequentially to a tibble named dat.
# Strategy 1
dat_1 <- func_1(dat)
dat_2 <- func_2(dat_1)
dat_final <- func_3(dat_2)
# Strategy 2
dat_final <- func_3(func_2(func_1(dat)))Both are hard to read and the first strategy is particularly prone to
errors as you have introduce several temporary tibbles with the same
name plus a numeric suffix – it’s very easy to make mistakes like
dat_2 <- func_2(dat) or
dat_final <- func_2(dat_2), especially if you are
copying-and-pasting lines and then changing suffixes. The second
strategy is ugly because we’re generally not used to reading things from
inside-out or right-to-left. It becomes especially problematic when each
function has many additional arguments.
Luckily there’s another option – the pipe operator
%>%. Here is what the same example looks like using the
pipe:
Let’s break down what’s happening on the right-hand side of the
assignment operator. First, R “pipes” the tbl dat into into
the function function func_1(). Then it pipes the result of
evaluating func_1(dat) into func_2() and so on
and so forth. One way to understand the pipe operator is to think of
your analysis as a “pipeline”. The sequence of analysis flow naturally
top-to-bottom and puts the emphasis on the actions being
carried out by the analyst (i.e. the functions) and the final output
rather than a bunch of temporary tbl’s that may not be of much
interest.
There are several conventions for formating code when using the pipe. See here and here for much more information and for some advanced “special” pipes.
The Lahman Baseball Database
As mentioned above, we will use data from a baseball data maintained by Sean Lahman. This database contains pitching, hitting, and fielding statistics from Major League Baseball from 1871 to 2016. The data is available as an R package, which we will need to install and load. To install the package, we need to run the following in our console.
Once the package is installed, we can load it into R along with the tidyverse packages:
As we know, many packages not only contain new functions, but also
new datasets. Whenever we load a package, the datasets that are part of
the package get implicitly loaded into the background. To see which
datasets come with the Lahman package, we use the data()
function.
This will open up a new window with all of the names of the datasets
contained in the Lahman package. Today, we will specifically be focusing
on the dataset called Pitching, which contains season-level
statistics on all pitchers going all the way back to 1871. Let’s load
this dataset as a tibble (which is easier to read than the default
data.frame) called pitching.
## # A tibble: 51,368 × 30
## playerID yearID stint teamID lgID W L G GS CG SHO SV
## <chr> <int> <int> <fct> <fct> <int> <int> <int> <int> <int> <int> <int>
## 1 aardsda01 2004 1 SFN NL 1 0 11 0 0 0 0
## 2 aardsda01 2006 1 CHN NL 3 0 45 0 0 0 0
## 3 aardsda01 2007 1 CHA AL 2 1 25 0 0 0 0
## 4 aardsda01 2008 1 BOS AL 4 2 47 0 0 0 0
## 5 aardsda01 2009 1 SEA AL 3 6 73 0 0 0 38
## 6 aardsda01 2010 1 SEA AL 0 6 53 0 0 0 31
## 7 aardsda01 2012 1 NYA AL 0 0 1 0 0 0 0
## 8 aardsda01 2013 1 NYN NL 2 2 43 0 0 0 0
## 9 aardsda01 2015 1 ATL NL 1 1 33 0 0 0 0
## 10 aasedo01 1977 1 BOS AL 6 2 13 13 4 2 0
## # ℹ 51,358 more rows
## # ℹ 18 more variables: IPouts <int>, H <int>, ER <int>, HR <int>, BB <int>,
## # SO <int>, BAOpp <dbl>, ERA <dbl>, IBB <int>, WP <int>, HBP <int>, BK <int>,
## # BFP <int>, GF <int>, R <int>, SH <int>, SF <int>, GIDP <int>There are tons of rows and columns in the dataset. For this exercise, we will only want to focus on ERA and also focus only on those pitchers who have pitched at least 150 innings. Unfortunately, the Lahman pitching dataset does not contain the number of innings pitched (IP). Instead, it has a column called “IPouts”, which is the number of outs pitched and whose formula is \(\text{IPOuts} = 3 \times \text{IP}.\)
Using the pipe and the dplyr verbs we learned in Lecture 2, we will create a new dataset called
pitching (we make it all lowercase to differentiate from
the original Lahman Pitching dataset), then add the “IP”
column, filter the data to include only all players who pitched at least
150 innings and played in either the AL or the NL, and select only the
columns corresponding to the player, year, team, league, innings
pitched, and ERA.
pitching <- pitching %>%
mutate(IP = IPouts/3) %>%
filter(lgID %in% c('AL', 'NL') & IP >= 150) %>%
select(playerID, yearID, teamID, lgID, IP, ERA)
pitching## # A tibble: 9,688 × 6
## playerID yearID teamID lgID IP ERA
## <chr> <int> <fct> <fct> <dbl> <dbl>
## 1 aasedo01 1978 CAL AL 179. 4.03
## 2 aasedo01 1979 CAL AL 185. 4.81
## 3 aasedo01 1980 CAL AL 175 4.06
## 4 abbeybe01 1892 WAS NL 196. 3.45
## 5 abbeybe01 1896 BRO NL 164. 5.15
## 6 abbotgl01 1977 SEA AL 204. 4.45
## 7 abbotgl01 1978 SEA AL 155. 5.27
## 8 abbotgl01 1980 SEA AL 215 4.1
## 9 abbotji01 1989 CAL AL 181. 3.92
## 10 abbotji01 1990 CAL AL 212. 4.51
## # ℹ 9,678 more rowsIMPORTANT: Before reading any further, make sure you and your team understand completely what is happening in the code above.
Now that we have ERA for all pitchers eligible for our analysis, we can plot the ERAs by year.
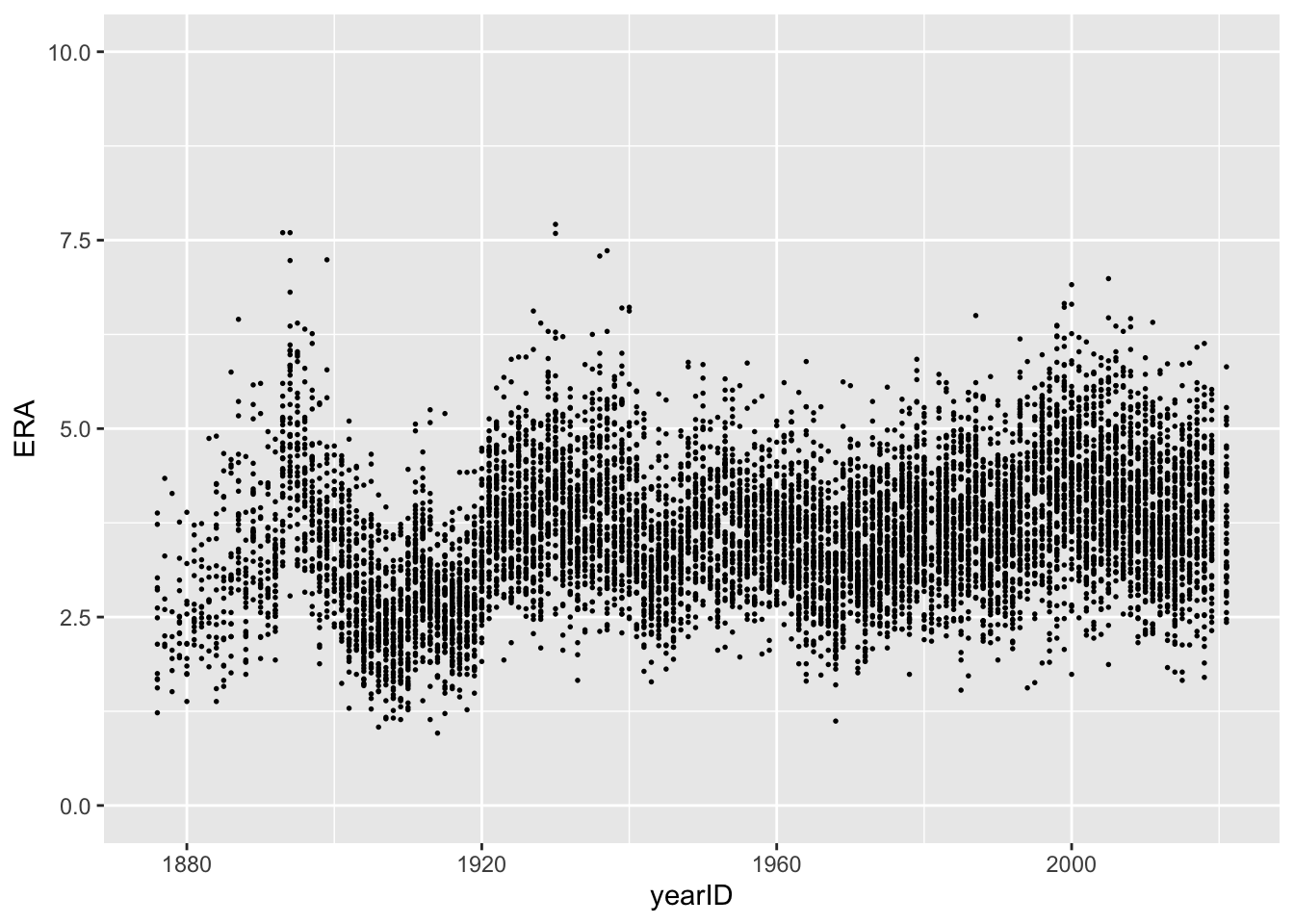
Looking at the plot, it appears that some of the pitchers from the
first few decades of baseball had the lowest ERA. Using
arrange() and slice_head(), we can see the 10
best pitchers.
## # A tibble: 10 × 6
## playerID yearID teamID lgID IP ERA
## <chr> <int> <fct> <fct> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96
## 2 brownmo01 1906 CHN NL 277. 1.04
## 3 gibsobo01 1968 SLN NL 305. 1.12
## 4 johnswa01 1913 WS1 AL 346 1.14
## 5 mathech01 1909 NY1 NL 275. 1.14
## 6 pfiesja01 1907 CHN NL 195 1.15
## 7 jossad01 1908 CLE AL 325 1.16
## 8 lundgca01 1907 CHN NL 207 1.17
## 9 alexape01 1915 PHI NL 376. 1.22
## 10 bradlge01 1876 SL3 NL 573 1.23It would appear that the best pitching season of all time was Dutch Leonard’s 1914 season with the Red Sox. The next best was Mordecai Brown’s 1906 season with the Cubs. How much better was Leonard’s 0.96 ERA than Brown’s 1.04 ERA?
To answer this, we transform ERA to standardized units using the
scale() function within a mutate(). We name
the new column zERA_all.
## # A tibble: 9,688 × 7
## playerID yearID teamID lgID IP ERA zERA_all[,1]
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96 -3.01
## 2 brownmo01 1906 CHN NL 277. 1.04 -2.92
## 3 gibsobo01 1968 SLN NL 305. 1.12 -2.83
## 4 johnswa01 1913 WS1 AL 346 1.14 -2.81
## 5 mathech01 1909 NY1 NL 275. 1.14 -2.81
## 6 pfiesja01 1907 CHN NL 195 1.15 -2.80
## 7 jossad01 1908 CLE AL 325 1.16 -2.78
## 8 lundgca01 1907 CHN NL 207 1.17 -2.77
## 9 alexape01 1915 PHI NL 376. 1.22 -2.72
## 10 bradlge01 1876 SL3 NL 573 1.23 -2.71
## # ℹ 9,678 more rowsNow we see that Leonard’s 0.96 ERA was about 3 standard deviations below the overall mean of qualified pitchers, while Brown’s was about 2.91 standard deviations below the mean. On the other hand, the ostensibly worst pitching season was Philadelphia’s own Les Sweetland in 1930. Incidentally enough, Sweetland started that season with a three-hit shutout! Check out this ESPN blog post about the 1930’s Phillies pitching staff.
Of course, you might argue that comparing the raw ERAs across the various years is somewhat unfair. After all, the game as it was played in 1914 is very different to the one played today! As such, it may be more appropriate to standardize all of the ERAs within each season separately. To do this, we will have to compute the mean and standard deviation of ERAs within each season.
Grouped Calculations
Before proceeding, let’s think for a minute about what the following code does:
Very often in a data analysis, instead of performing a calculation on the entire data set, you’ll want to first split the data into smaller subsets, apply the same calculation on every subset, and then combine the results from each subset. For example, in order to replicate the figure above from Prof. Wyner’s lecture, we need to split our pitching dataset based on the year, compute the average ERA within each year, and then combine these into a single tibble.
One strength of dplyr (one of the packages within the
tidyverse) is the ease with which you can follow this
“split-apply-combine” paradigm using the function
group_by(). We can use this in concert with the pipe as
follows.
When we print out pitching now, we notice an extra line
that tells us the grouping variable. Now when we pass this tibble on to
subsequent calculations, these calculations will be done on each group.
Recall from earlier that the code
pitching %>% reframe(mean = mean(ERA)) returned a single
row containing the average of ERA over all players and year. If we now
run the same code again, we actually get a tibble with one row per year
that lists the mean and standard deviation of ERA within each
year. We will save this tibble as
pitching_summary:
In Lecture 2, we listed a few useful
functions to be used within reframe(). One of them,
n(), returns counts and is especially useful when used on a
grouped tibble. We can, for instance, count the number of pitchers in
our dataset within each year using n().
## # A tibble: 147 × 2
## yearID count
## <int> <int>
## 1 1877 7
## 2 1878 7
## 3 1880 12
## 4 1876 13
## 5 1879 13
## 6 1883 13
## 7 1881 14
## 8 1882 14
## 9 1884 19
## 10 1885 19
## # ℹ 137 more rowsExercise: Describe, in words, what the following code does.
Once we add a grouping to our tibble, it also changes the way
mutate() operates on the tibble. We can now standardize
each pitcher’s ERA within each year and save that result in a column
called zERA_year.
## # A tibble: 9,688 × 8
## # Groups: yearID [147]
## playerID yearID teamID lgID IP ERA zERA_all zERA_year[,1]
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96 -3.01 -3.48
## 2 martipe02 2000 BOS AL 217 1.74 -2.13 -3.16
## 3 maddugr01 1995 ATL NL 210. 1.63 -2.25 -3.02
## 4 luquedo01 1923 CIN NL 322 1.93 -1.91 -2.88
## 5 martipe02 1999 BOS AL 213. 2.07 -1.75 -2.85
## 6 brownke01 1996 FLO NL 233 1.89 -1.96 -2.82
## 7 eichhma01 1986 TOR AL 157 1.72 -2.15 -2.81
## 8 maddugr01 1994 ATL NL 202 1.56 -2.33 -2.79
## 9 piercbi02 1955 CHA AL 206. 1.97 -1.87 -2.77
## 10 hubbeca01 1933 NY1 NL 309. 1.66 -2.22 -2.77
## # ℹ 9,678 more rowsUngrouping and Grouping on Multiple Variables
As we just saw, when we add a grouping to a tbl, it affects how verbs
like reframe() and mutate() operate on our
data. It is sometimes the case that we wish to remove the grouping and
let these verbs (and others) operate on the entire dataset again. To
remove the grouping, we have to use the ungroup() function.
Remember, as with the other dplyr verbs we’ve learned, we need to save
the result if we want the tbl to remain ungrouped!
To verify that we’ve indeed removed the grouping, let’s re-run the code from above to compute the mean and standard deviation of ERA.
## # A tibble: 1 × 2
## mean sd
## <dbl> <dbl>
## 1 3.61 0.881Up to this point, we have only grouped on a single variable. It is sometimes desirable to group on multiple variables at once. For instance, we may want to standardize ERA not only within each year but also within each league (AL and NL). That is, we may want to standardize each individual pitcher’s ERA using only the data from the other pitchers who pitched in the same league and in the same season. We also add a column called count_year_lg to record the number of pitchers included in each year-league combination.
pitching <-
pitching %>%
group_by(yearID, lgID) %>%
mutate(zERA_year_lg = scale(ERA),
count_year_lg = n())
pitching## # A tibble: 9,688 × 10
## # Groups: yearID, lgID [269]
## playerID yearID teamID lgID IP ERA zERA_all zERA_year zERA_year_lg[,1]
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 aasedo01 1978 CAL AL 179. 4.03 0.473 0.741 0.506
## 2 aasedo01 1979 CAL AL 185. 4.81 1.36 1.42 1.10
## 3 aasedo01 1980 CAL AL 175 4.06 0.507 0.466 0.428
## 4 abbeybe01 1892 WAS NL 196. 3.45 -0.185 0.524 0.524
## 5 abbeybe01 1896 BRO NL 164. 5.15 1.74 1.23 1.23
## 6 abbotgl01 1977 SEA AL 204. 4.45 0.950 1.05 1.24
## 7 abbotgl01 1978 SEA AL 155. 5.27 1.88 2.59 2.26
## 8 abbotgl01 1980 SEA AL 215 4.1 0.553 0.529 0.499
## 9 abbotji01 1989 CAL AL 181. 3.92 0.348 0.626 0.288
## 10 abbotji01 1990 CAL AL 212. 4.51 1.02 1.16 0.965
## # ℹ 9,678 more rows
## # ℹ 1 more variable: count_year_lg <int>When we arrange by the ERA standardized within the year and league, we now see that Pedro Martinez’s 1999 and 2000 season with the Red Sox were even better than Dutch Leonard’s 1914 season!
As a final note, when we group by multiple variables, the order in
which we specify the variables in group_by() matters.
Back to the figure
We started this module with a figure similar to one from Professor Wyner’s class that plotted ERAs over time. When we run the following code, we get a plot that’s very similar to the desired one but that is missing the red line showing the average ERA within each season.
To add this to our plot, we need to simply re-run the code
above but with some additional calls to geom_line.
ggplot(pitching) +
geom_point(aes(x = yearID, y = ERA), size = 0.3) +
ylim(0, 10) +
geom_line(data = pitching_summary, mapping = aes(x = yearID, y = mean), col = 'red')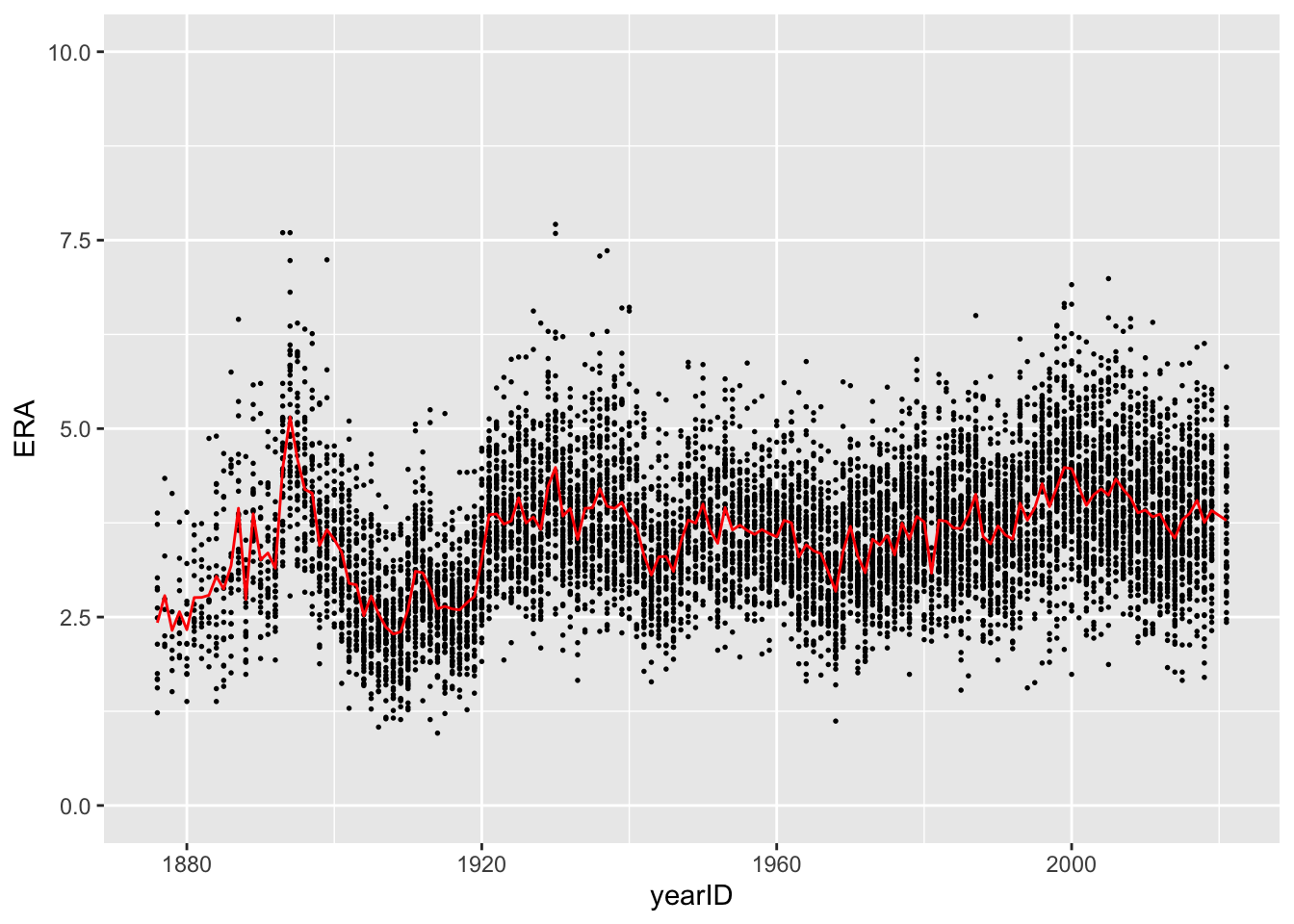
You’ll notice that the last line of code is a bit different than
anything we’ve seen before. In particular, we are specifying both the
data and mapping within the same ggplot2 function. If all of the
information we want to include in the plot is coming from the same data
source, it’s enough to just specify the data argument in
the first line, like we do with ggplot(data = pitching) and
not in every subsequent call to functions like geom_point
or geom_line. However, whenever we want to add layers to a
plot using data from another source (in this case, using data from
pitching_summary to plot the average ERAs), we need to tell
R explicitly and specify the data argument in
geom_line.
