Lecture 4: Defining custom functions and standardizing data
Introduction
On day 3 of the morning lectures (Lecture 6), you see a graph of Earned Run Average (ERA) against year, along with a line connecting the average ERA in each year.
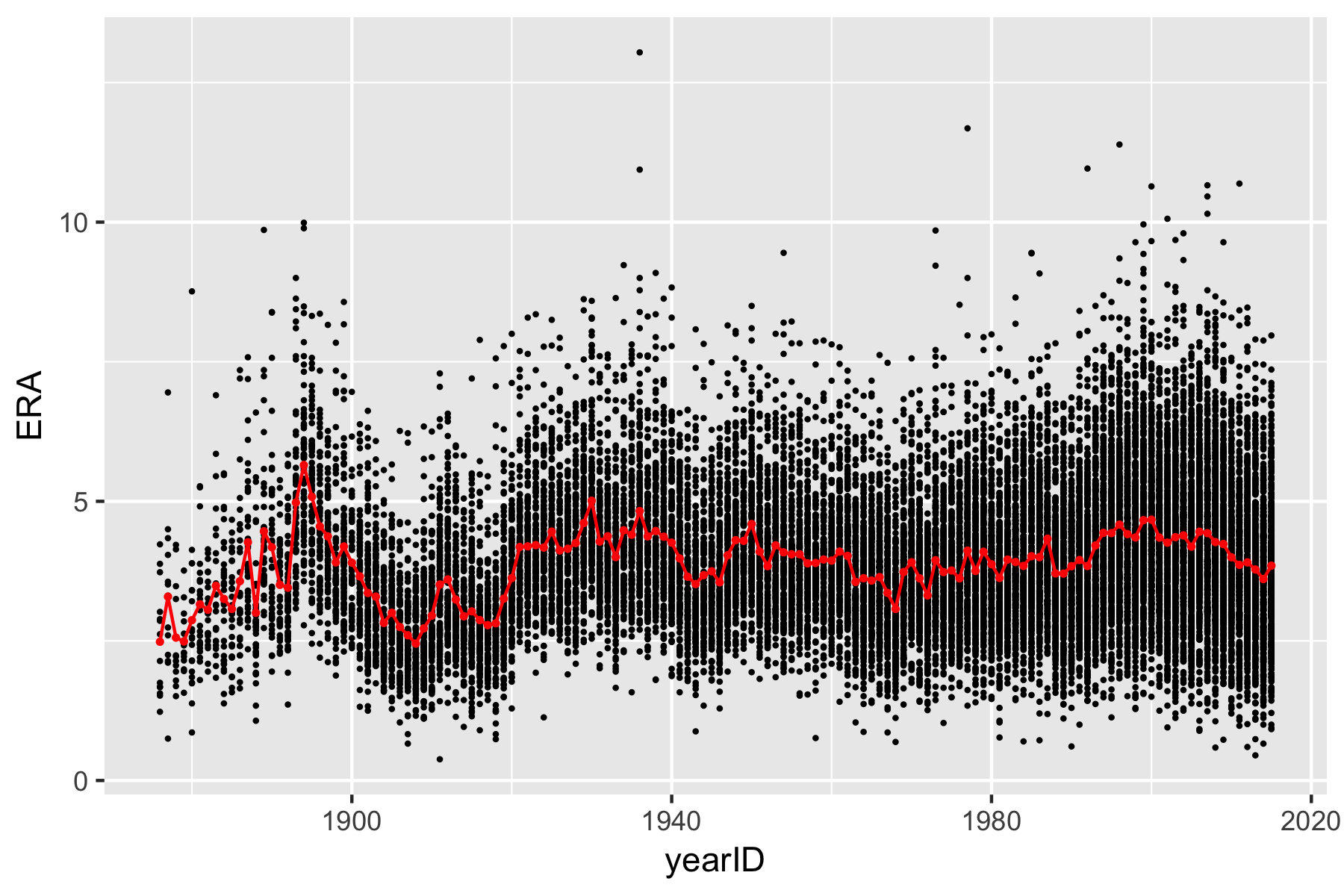
In order to reproduce this image, we will work with the Lahman Baseball
Database. As it turns out, there is an R package that includes the
entire database (up until the 2018 season). We will load that into R
along with the tidyverse packages when we begin our
analysis.
The Lahman Baseball Database
As mentioned above, we will use data from a baseball data maintained by Sean Lahman. This database contains pitching, hitting, and fielding statistics from Major League Baseball from 1871 to 2016. The data is available as an R package, which we will need to install and load. To install the package, we need to run the following in our console.
Once the package is installed, we can load it into R along with the tidyverse packages:
As we know, many packages not only contain new functions, but also
new datasets. Whenever we load a package, the datasets that are part of
the package get implicitly loaded into the background. To see which
datasets come with the Lahman package, we use the data()
function.
This will open up a new window with all of the names of the datasets
contained in the Lahman package. Today, we will specifically be focusing
on the dataset called Pitching, which contains season-level
statistics on all pitchers going all the way back to 1871. Let’s load
this dataset as a tibble (which is easier to read than the default
data.frame) called pitching.
## # A tibble: 49,430 × 30
## playerID yearID stint teamID lgID W L G GS CG SHO SV
## <chr> <int> <int> <fct> <fct> <int> <int> <int> <int> <int> <int> <int>
## 1 bechtge01 1871 1 PH1 NA 1 2 3 3 2 0 0
## 2 brainas01 1871 1 WS3 NA 12 15 30 30 30 0 0
## 3 fergubo01 1871 1 NY2 NA 0 0 1 0 0 0 0
## 4 fishech01 1871 1 RC1 NA 4 16 24 24 22 1 0
## 5 fleetfr01 1871 1 NY2 NA 0 1 1 1 1 0 0
## 6 flowedi01 1871 1 TRO NA 0 0 1 0 0 0 0
## 7 mackde01 1871 1 RC1 NA 0 1 3 1 1 0 0
## 8 mathebo01 1871 1 FW1 NA 6 11 19 19 19 1 0
## 9 mcbridi01 1871 1 PH1 NA 18 5 25 25 25 0 0
## 10 mcmuljo01 1871 1 TRO NA 12 15 29 29 28 0 0
## # … with 49,420 more rows, and 18 more variables: IPouts <int>, H <int>,
## # ER <int>, HR <int>, BB <int>, SO <int>, BAOpp <dbl>, ERA <dbl>, IBB <int>,
## # WP <int>, HBP <int>, BK <int>, BFP <int>, GF <int>, R <int>, SH <int>,
## # SF <int>, GIDP <int>There are tons of rows and columns in the dataset. For this exercise, we will only want to focus on ERA and also focus only on those pitchers who have pitched at least 150 innings. Unfortunately, the Lahman pitching dataset does not contain the number of innings pitched (IP). Instead, it has a column called “IPouts”, which is the number of outs pitched and whose formula is \(\text{IPOuts} = 3 \times \text{IP}.\)
Using the pipe and the dplyr verbs we learned in Lecture 2, we will create a new dataset called
pitching (we make it all lowercase to differentiate from
the original Lahman Pitching dataset), then add the “IP”
column, filter the data to include only all players who pitched at least
150 innings and played in either the AL or the NL, and select only the
columns corresponding to the player, year, team, league, innings
pitched, and ERA.
pitching <- pitching %>%
mutate(IP = IPouts/3) %>%
filter(lgID %in% c('AL', 'NL') & IP >= 150) %>%
select(playerID, yearID, teamID, lgID, IP, ERA)
pitching## # A tibble: 9,577 × 6
## playerID yearID teamID lgID IP ERA
## <chr> <int> <fct> <fct> <dbl> <dbl>
## 1 bondto01 1876 HAR NL 408 1.68
## 2 bordejo01 1876 BSN NL 218. 2.89
## 3 bradlfo01 1876 BSN NL 173. 2.49
## 4 bradlge01 1876 SL3 NL 573 1.23
## 5 cummica01 1876 HAR NL 216 1.67
## 6 deando01 1876 CN1 NL 263. 3.73
## 7 devliji01 1876 LS1 NL 622 1.56
## 8 fishech01 1876 CN1 NL 229. 3.02
## 9 knighlo01 1876 PHN NL 282 2.62
## 10 mannija01 1876 BSN NL 197. 2.14
## # … with 9,567 more rowsIMPORTANT: Before reading any further, make sure you and your team understand completely what is happening in the code above.
Now that we have ERA for all pitchers eligible for our analysis, we can plot the ERAs by year.
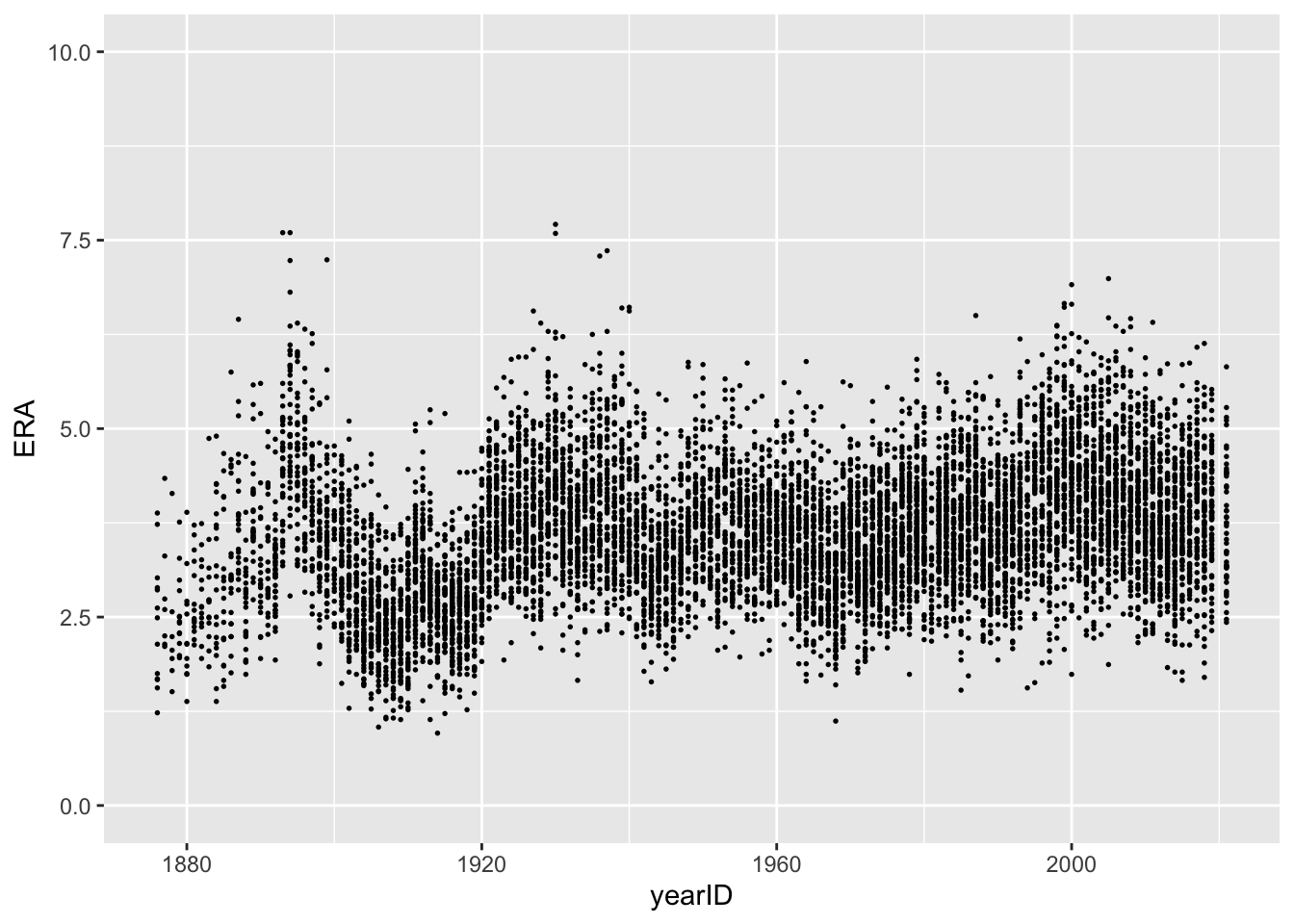
Looking at the plot, it appears that some of the pitchers from the
first few decades of baseball had the lowest ERA. Using
arrange(), we can see which pitcher had the best season
according to ERA.
## # A tibble: 9,577 × 6
## playerID yearID teamID lgID IP ERA
## <chr> <int> <fct> <fct> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96
## 2 brownmo01 1906 CHN NL 277. 1.04
## 3 gibsobo01 1968 SLN NL 305. 1.12
## 4 mathech01 1909 NY1 NL 275. 1.14
## 5 johnswa01 1913 WS1 AL 346 1.14
## 6 pfiesja01 1907 CHN NL 195 1.15
## 7 jossad01 1908 CLE AL 325 1.16
## 8 lundgca01 1907 CHN NL 207 1.17
## 9 alexape01 1915 PHI NL 376. 1.22
## 10 bradlge01 1876 SL3 NL 573 1.23
## # … with 9,567 more rowsIt would appear that the best pitching season of all time was Dutch Leonard’s 1914 season with the Red Sox. The next best was Mordecai Brown’s 1906 season with the Cubs. How much better was Leonard’s 0.96 ERA than Brown’s 1.04 ERA?
To answer this, we can transform ERA to standardized units using the
mutate() function. There is a minor complication: there is
not a built-in function for standardizing a variable in R! Luckily for
us, R allows us to define our own functions like so:
standardize <- function(x){
mu <- mean(x, na.rm = TRUE)
sigma <- sd(x, na.rm = TRUE)
return( (x - mu)/sigma )
}For now, don’t worry too much about the syntax or the
na.rm = TRUE bits; we will discuss them in more depth
later. Armed with our standardize() function, we can add a
column called zERA_all which transforms ERA to the standardized
scale.
## # A tibble: 9,577 × 7
## playerID yearID teamID lgID IP ERA zERA_all
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96 -3.01
## 2 brownmo01 1906 CHN NL 277. 1.04 -2.92
## 3 gibsobo01 1968 SLN NL 305. 1.12 -2.83
## 4 mathech01 1909 NY1 NL 275. 1.14 -2.81
## 5 johnswa01 1913 WS1 AL 346 1.14 -2.81
## 6 pfiesja01 1907 CHN NL 195 1.15 -2.79
## 7 jossad01 1908 CLE AL 325 1.16 -2.78
## 8 lundgca01 1907 CHN NL 207 1.17 -2.77
## 9 alexape01 1915 PHI NL 376. 1.22 -2.71
## 10 bradlge01 1876 SL3 NL 573 1.23 -2.70
## # … with 9,567 more rowsNow we see that Leonard’s 0.96 ERA was about 3 standard deviations below the overall mean of qualified pitchers, while Brown’s was about 2.91 standard deviations below the mean. On the other hand, the ostensibly worst pitching season was Philadelphia’s own Les Sweetland in 1930. Incidentally enough, Sweetland started that season with a three-hit shutout! Check out this ESPN blog post about the 1930’s Phillies pitching staff.
Of course, you might argue that comparing the raw ERAs across the various years is somewhat unfair. After all, the game as it was played in 1914 is very different to the one played today! As such, it may be more appropriate to standardize all of the ERAs within each season separately. To do this, we will have to compute the mean and standard deviation of ERAs within each season.
Grouped calculations
Very often in a data analysis, instead of performing a calculation on the entire data set, you’ll want to first split the data into smaller subsets, apply the same calculation on every subset, and then combine the results from each subset. For example, in order to replicate the figure above from Prof. Wyner’s lecture, we need to split our pitching dataset based on the year, compute the average ERA within each year, and then combine these into a single tibble.
One strength of dplyr is the ease with which you can follow this
“split-apply-combine” paradigm using the function
group_by(). We can use this in concert with the pipe as
follows:
When we print out pitching now, we notice an extra line
that tells us the grouping variable. Now when we pass this dataset on to
subsequent calculations, these calculations will be done on each
group.
We can now summarize each season using another tidyverse
function called… summarize()! This convenient function will
compute summary statistics that we specify with respect to the groups
from group_by(). For instance, we can compute the average
ERA in each year in the following way:
## # A tibble: 145 × 2
## yearID ave_ERA
## <int> <dbl>
## 1 1876 2.42
## 2 1877 2.78
## 3 1878 2.32
## 4 1879 2.57
## 5 1880 2.33
## 6 1881 2.76
## 7 1882 2.76
## 8 1883 2.79
## 9 1884 3.04
## 10 1885 2.87
## # … with 135 more rowsThe following functions are quite useful for summarizing several aspects of the distribution of the variables in our dataset:
- Center:
mean(),median() - Spread:
sd(),IQR() - Range:
min(),max() - Count:
n(),n_distinct()
We’ll now create a dataset, pitching_summary, that
contains the mean and standard deviation of ERA within each
year:
One of the most commonly used functions, n(), returns
counts and is especially useful when used on a grouped dataset We can,
for instance, count the number of pitchers in our dataset within each
year using n().
## # A tibble: 145 × 2
## yearID count
## <int> <int>
## 1 1877 7
## 2 1878 7
## 3 1880 12
## 4 1876 13
## 5 1879 13
## 6 1883 13
## 7 1881 14
## 8 1882 14
## 9 1884 19
## 10 1885 19
## # … with 135 more rowsOr equivalently, we can use the count function:
## # A tibble: 145 × 2
## # Groups: yearID [145]
## yearID n
## <int> <int>
## 1 1877 7
## 2 1878 7
## 3 1880 12
## 4 1876 13
## 5 1879 13
## 6 1883 13
## 7 1881 14
## 8 1882 14
## 9 1884 19
## 10 1885 19
## # … with 135 more rowsWhat’s the difference between the two approaches above?
Exercise: Describe, in words, what the following code does.
Once we add a grouping to our dataset, it also changes the way
mutate() operates on it. We can now standardize each
pitcher’s ERA within each year and store that result in a column called
z_era_year.
## # A tibble: 9,577 × 8
## # Groups: yearID [145]
## playerID yearID teamID lgID IP ERA zERA_all z_era_year
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl> <dbl>
## 1 leonadu01 1914 BOS AL 225. 0.96 -3.01 -3.48
## 2 martipe02 2000 BOS AL 217 1.74 -2.12 -3.16
## 3 maddugr01 1995 ATL NL 210. 1.63 -2.25 -3.02
## 4 luquedo01 1923 CIN NL 322 1.93 -1.91 -2.88
## 5 martipe02 1999 BOS AL 213. 2.07 -1.75 -2.85
## 6 brownke01 1996 FLO NL 233 1.89 -1.95 -2.82
## 7 eichhma01 1986 TOR AL 157 1.72 -2.15 -2.81
## 8 maddugr01 1994 ATL NL 202 1.56 -2.33 -2.79
## 9 piercbi02 1955 CHA AL 206. 1.97 -1.86 -2.77
## 10 hubbeca01 1933 NY1 NL 309. 1.66 -2.22 -2.77
## # … with 9,567 more rowsUngrouping and grouping on multiple variables
As we just saw, when we add a grouping to a dataset, it affects how
verbs like summarize() and mutate() operate on
our data. It is sometimes the case that we wish to remove the grouping
and let these verbs (and others) operate on the entire dataset again. To
remove the grouping, we have to use the ungroup() function.
Remember, as with the other tidyverse verbs we’ve learned,
we need to store the result if we want the dataset to remain
ungrouped!
To verify that we’ve indeed removed the grouping, let’s re-run the code from above to compute the mean and standard deviation of ERA.
## # A tibble: 1 × 2
## mean sd
## <dbl> <dbl>
## 1 3.61 0.881Up to this point, we have only grouped on a single variable. It is
sometimes desirable to group on multiple variables at once. For
instance, we may want to standardize ERA not only within each year but
also within each leauge (AL and NL). That is, we may want to standardize
each individual pitcher’s ERA using only the data from the other
pitchers who pitched in the same league and in the same season. We also
add a column called count_year_lg to record the number of
pitchers included in each year-league combination.
pitching <- pitching %>%
group_by(yearID, lgID) %>%
mutate(z_era_year_lg = standardize(ERA),
count = n())When we arrange by the ERA standardized within the year and league, we now see that Pedro Martinez’s 1999 and 2000 season with the Red Sox were even better than Dutch Leonard’s 1914 season!
## # A tibble: 9,577 × 10
## # Groups: yearID, lgID [265]
## playerID yearID teamID lgID IP ERA zERA_all z_era_year z_era_year_lg
## <chr> <int> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 martipe02 2000 BOS AL 217 1.74 -2.12 -3.16 -3.55
## 2 martipe02 1999 BOS AL 213. 2.07 -1.75 -2.85 -3.15
## 3 leonadu01 1914 BOS AL 225. 0.96 -3.01 -3.48 -3.13
## 4 eichhma01 1986 TOR AL 157 1.72 -2.15 -2.81 -3.06
## 5 youngcy01 1901 BOS AL 371. 1.62 -2.26 -2.51 -2.81
## 6 alexape01 1915 PHI NL 376. 1.22 -2.71 -2.28 -2.78
## 7 maddugr01 1995 ATL NL 210. 1.63 -2.25 -3.02 -2.75
## 8 gibsobo01 1968 SLN NL 305. 1.12 -2.83 -2.73 -2.75
## 9 grovele01 1931 PHA AL 289. 2.06 -1.76 -2.39 -2.74
## 10 guidrro01 1978 NYA AL 274. 1.74 -2.12 -2.67 -2.73
## # … with 9,567 more rows, and 1 more variable: count <int>As a final note, when we group by multiple variables, the order in
which we specify the variables in group_by() matters.
Back to the figure
We started this module with a figure similar to one from Professor Wyner’s class that plotted ERAs over time. When we previously ran the following code, we got a plot that’s very similar to the desired one but that is missing the red line showing the average ERA within each season.
To add the red line to our plot, we need to simply re-run the code
above but with some additional calls to geom_line.
ggplot(pitching) +
geom_point(aes(x = yearID, y = ERA), size = 0.3) +
ylim(0, 10) +
geom_line(data = pitching_summary,
aes(x = yearID, y = mean), col = 'red')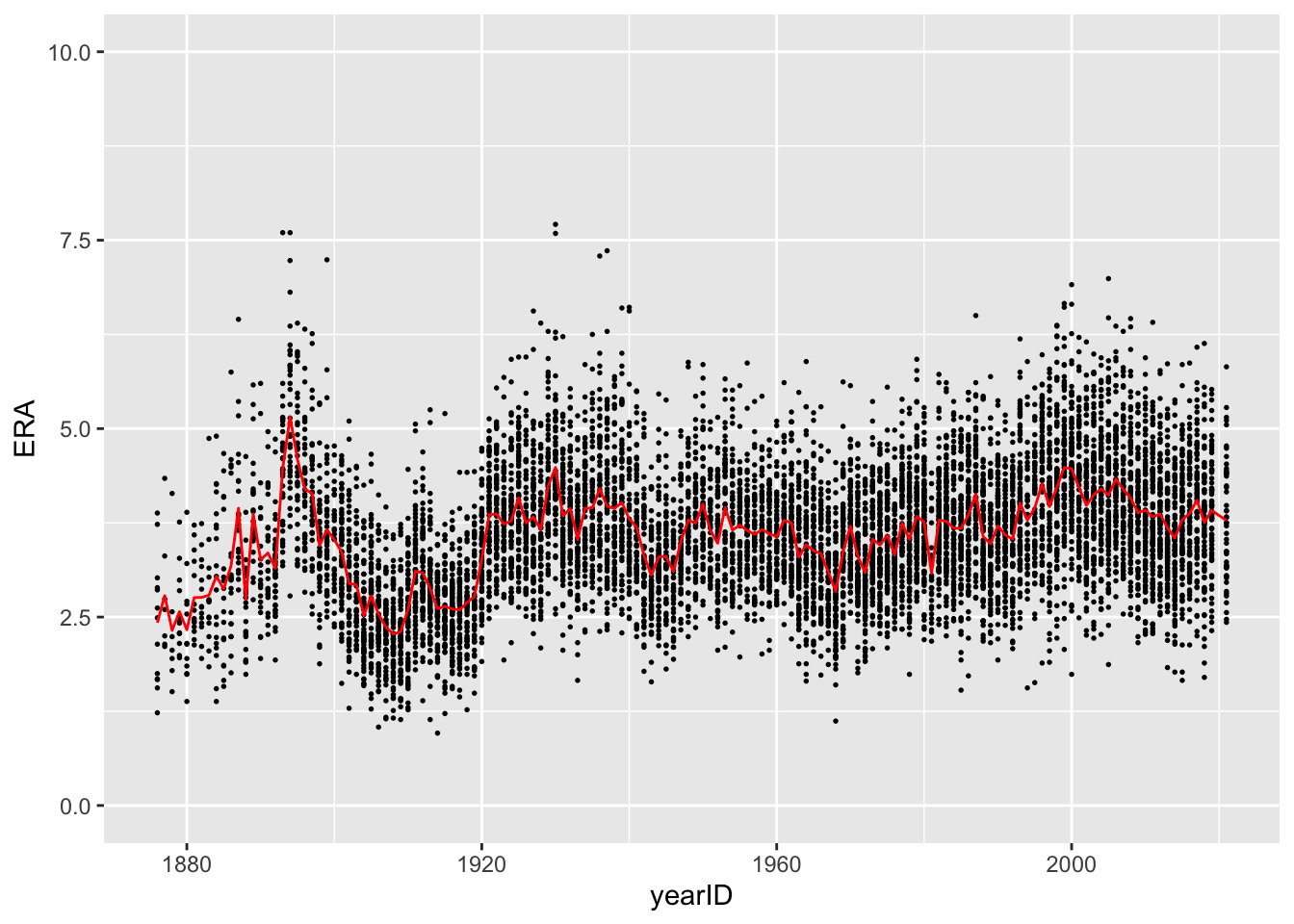
You’ll notice that the last line of code is a bit different than
anything we’ve seen before. In particular, we are specifying both the
data and mapping within the same ggplot2 function. If all of the
information we want to include in the plot is coming from the same data
source, it’s enough to just specify the data argument in
the first line, like we do with ggplot(data = pitching) and
not in every subsequent call to functions like geom_point
or geom_line. However, whenever we want to add layers to a
plot using data from another source (in this case, using data from
pitching_summary to plot the average ERAs), we need to tell
R explicitly and specify the data argument in
geom_line.